Afficher la correction

Actuelle

Autre

Retour

Imprimer

La conversions degrés Celsius-Farenheit

En voyage aux États-unis, on a relevé des températures avec un thermomètre français mais aussi avec un thermomètre acheté sur place.

On a relevé les différentes températures dans le tableau suivant :

Recherche d'un coefficient de proportionnalité

La plupart des unités sont convertibles via un coefficient de proportionnalité, autrement dit via la modélisation par une fonction linéaire.

1. Donner un exemple de conversion qui est modélisée par une fonction linéaire.

Pour passer de \(km\) à \(m\), on mutilplie par 1 000.

On peut donc imaginer une fonction \(C(x)\) tel que :

$$ C(x) = 1000x $$
2. Les données du tableau reflètent-ils une situation de proportionnalité ?

Pour les deux premières lignes, on cherche à savoir si :

$$ \frac{27}{8.5} = \frac{80.6}{47.3} \hspace{1em} ?$$

Ce n'est pas le cas, car :

$$ \frac{27 \times 47.3}{8.5} \approx 150.25 \neq 80.6 $$
3. Pourra-t-on alors modéliser cette conversion par une fonction linéaire ?

Non, car si on ne se trouve pas dans une situation de proportionnalité, on ne peut pas modéliser par une fonction linéaire (et inversement).

Construction de la courbe représentative et résolution graphique

1. Reporter sur le graphique suivant les données du tableau, puis tracer la courbe représentative.





2. Quelle semble être la nature de cette fonction ?

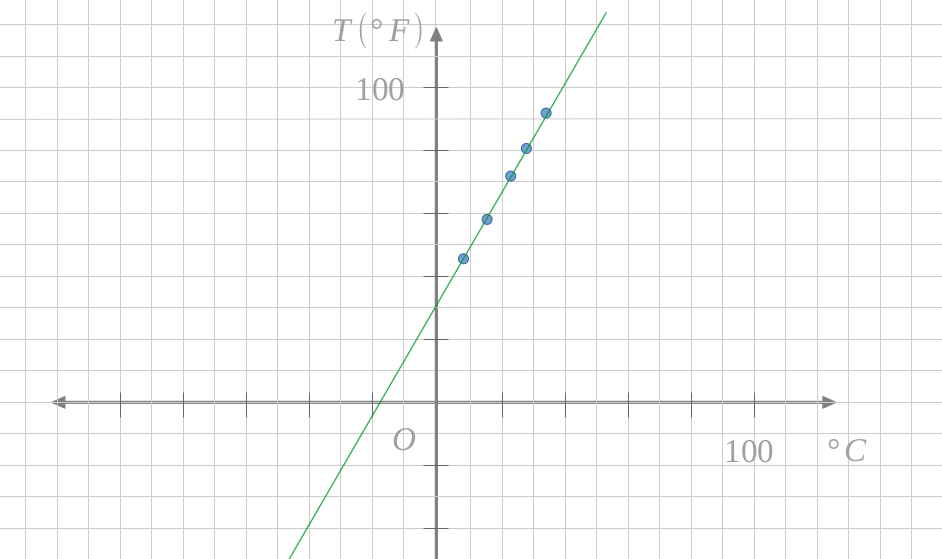
C'est une droite qui ne passe pas par l'origine, alors il semble que cela soit une fonction affine.

3. Selon cette courbe, quelle sera la température en degré \(\text{°F}\) si la température est de \(20 \text{ °C}\) ?

Sur le graphique, on lit approximativement \(68 \text{ °F}\).

Modélisation de la fonction

1. Comment calcule-t-on l'expression d'une fonction affine ?

On doit déterminer deux coefficients : \(a\) et \(b\).

Avec deux points de la courbe, on détermine d'abord \(a\) par :

$$ a = \frac{y_2 - y_1}{x_2 - x_1} $$

Ensuite, on détermine \(b\) en reprenant un des deux points, et en remplaçant \(a\) dans la formule :

$$ y_1 = a x_1 + b $$

$$ b = y_1 - a x_1 $$

Ensuite, la fonction sera modélisée par :

$$ f(x) = ax + b $$
2. Déterminer alors l'expression de la fonction correspondante à la courbe précédente.

Calculons la pente, puis l'ordonnée à l'origine.

1. Calcul de la pente \(a\)

Avec deux points \(P\bigl[ 27 ; 80.6 \bigr]\) et \(Q\bigl[ 8.5 ; 47.3 \bigr]\) des valeurs du tableau :

$$ a = \frac{47.3 - 80.6}{8.5-27} $$
$$ a = \frac{-33.3}{-18.5} $$
$$ a = \frac{9}{5} $$

2. Calcul de l'ordonnée à l'origine \(b\)

On utilise le point \(P\).

$$ 80.6 = \frac{9}{5} \times 27 + b $$
$$ 80.6 - \frac{9}{5} \times 27 = b $$
$$ b = 32 $$

3. Formule

On a alors :

$$ T_{F} = \frac{9}{5} T_{C} + 32 $$
3. Faire la calcul avec cette nouvelle formule, et retrouver le résultat de la question 2.c).

On démarre de la formule trouvée précédemment :

$$ T_{F} = \frac{9}{5} T_{C} + 32 $$

Pour \( T_{C} = 20 \text{ °C}\), on remplace :

$$ T_{F} = \frac{9}{5} \times 20 + 32 $$

$$ T_{F} = \frac{9 \times 4 \times \cancel{5}}{\cancel{5}} + 32 $$

$$ T_{F} = 36 + 32 $$

$$ T_{F} = 68 \text{ °F} $$

Modélisation inverse

1. Peut-on, à l'inverse, exprimer la conversion des degrés \(\text{ °F}\) vers les degrés \(\text{ °C}\) ?

On démarre de la formule trouvée précédemment :

$$ T_{F} = \frac{9}{5} T_{C} + 32 $$

Et on s'arrange pour isoler \(\text{ °C}\) :

$$ T_{F} \textcolor{#9F6A6A}{- 32} = \frac{9}{5} T_{C} + \underbrace{32 \textcolor{#9F6A6A}{- 32}} _\text{ = 0} $$

$$ T_{F} - 32 = \frac{9}{5} T_{C} $$

$$ \textcolor{#9F6A6A}{ \Bigl(} T_{F} - 32 \textcolor{#9F6A6A}{ \Bigr) \times \frac{5}{9}} = \underbrace{\frac{9}{5} \textcolor{#9F6A6A}{\times \frac{5}{9}} } _\text{ = 1} \times T_{C} $$

$$ \Bigl( T_{F} - 32 \Bigr) \times \frac{5}{9} = T_{C} $$

$$ T_{C} = \Bigl( T_{F} - 32 \Bigr) \times \frac{5}{9} $$
2. Peut-on arranger cette expression pour obtenir une fonction affine ?

En développant l'expression précédente, on obtient :

$$ T_{C} = \Bigl( T_{F} - 32 \Bigr) \times \frac{5}{9} $$

$$ T_{C} = \frac{5}{9} \times T_{F} - \frac{5}{9} \times 32 $$

$$ T_{C} = \frac{5}{9} T_{F} - \frac{160}{9} $$
3. Enfin, que valent alors les coefficients \(a\) et \(b\) ?

On obtient que :

$$ \left \{ \begin{gather*} a = \frac{5}{9} \\ b = - \frac{160}{9} \end{gather*} \right \} $$