Vider les textes à trous
Vider les graphiques
Retour
Imprimer
Une fonction linéaire est une fonction de type :
Elle modélise notamment une situation de proportionnalité .
À partir d'un nombre, on lui applique un coefficient :
N'importe quelle fonction linéaire sera représentée par une droite passant par l'origine \(\bigl(O\bigl[ 0 ; 0 \bigr] \bigr)\).
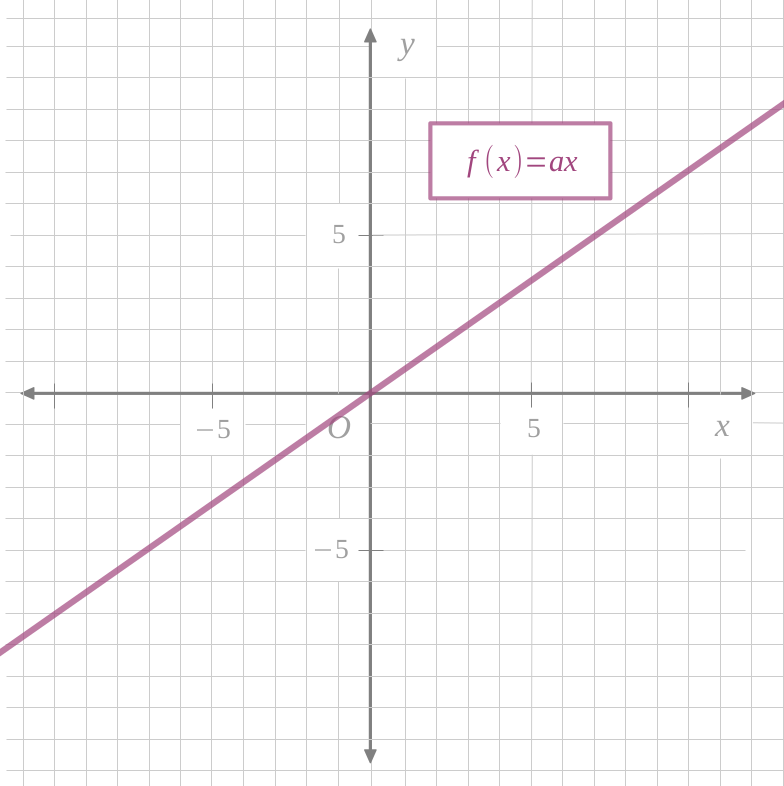
Le nombre \(a\) est appellé le coefficient directeur .
Graphiquement, le signe de \(a\) indique quelle sera l'inclinaison de la droite :
Une fonction affine est une fonction de type :
À partir d'un nombre, on lui applique en premier lieu un coefficient :
Puis, à partir de ce résultat, on lui ajoute un nombre :
Ce qui revient à faire :
N'importe quelle fonction affine sera représentée par une droite .
La différence avec une fonction affine, est que l'on en plus un nombre \(b\), que l'on appelle l'ordonnée à l'origine .
Algébriquement, \(b\) est l'image de la fonction \(f\) par \((x = 0)\) :
Graphiquement, \(b\) est la valeur de \(y\) que l'on lit au croisement de :
la courbe de la fonction d'étude
l'axe des abscisses \(\overrightarrow{O\textcolor{#9F6A6A}{j}}\)
On calcule ce coefficent grâce à deux points \(M_1\bigl( x_1 ; y_1 \bigr)\) et \(M_2\bigl[ x_2 ; y_2 \bigr]\) de la courbe :
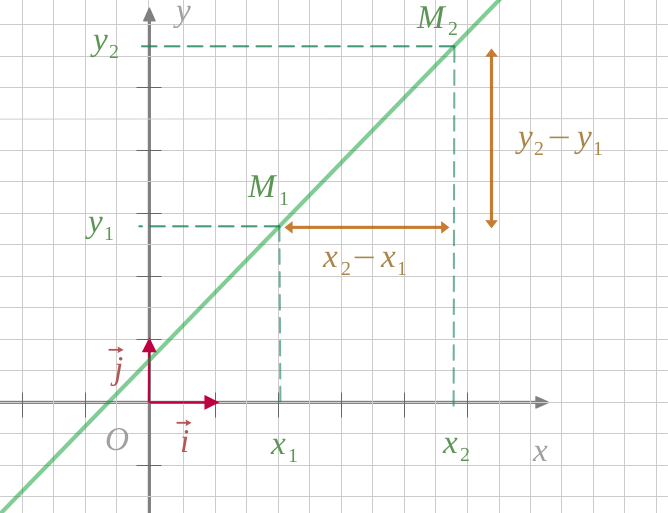
Exemple : avec deux points \(M_1\) et \(M_2\) de la droite :
Alors, le coefficient directeur vaut :
On en conclue que cette fonction est décroissante .
Après avoir déterminé \(a\), on reprend un des deux points qui nous a permis de le calculer, et on remplace pour isoler \(b\).
Exemple : en reprenant les deux même points \(M_1\) et \(M_2\) :
À partir de :
On remplace \((a = -1)\), ainsi que les valeurs \(\bigl[ x ; y \bigr]\) du point \(A\bigl[ 1 ; 3 \bigr]\) :
L'expression de notre fonction est donc :