Imprimer
Vider les textes à trous
Vider les graphiques
Actuelle
Autre
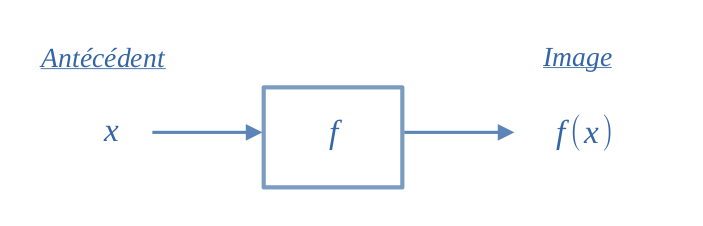
Une fonction est une opération qui transforme un nombre \(x\), en une image unique \(f(x)\).
De manière générale, on écrira pour définir une fonction avec comme variable \(x\) :
« une fonction \(f\), qui associe à un antécédent \(x\) une image \(f(x)\) »
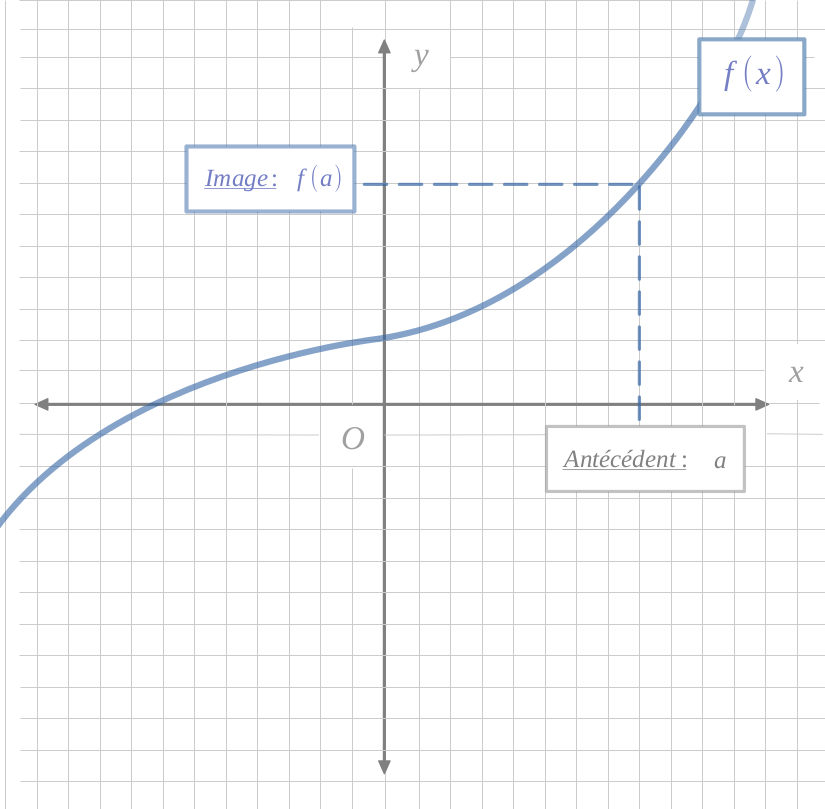
Les antécédents se situent sur l'axe horizontal \(x\).
Les images se situent sur l'axe vertical \(y\).
Lorsqu'on a qu'une seule courbe sur un graphique, on peut noter l'image générale : \(y = f(x)\).
Soit un intervalle \( I = \bigl[ a,b \bigr] \).
Fonctions croissantes
On dit qu'une fonction est croissante si les images sont rangées dans le même ordre que les antécédents.
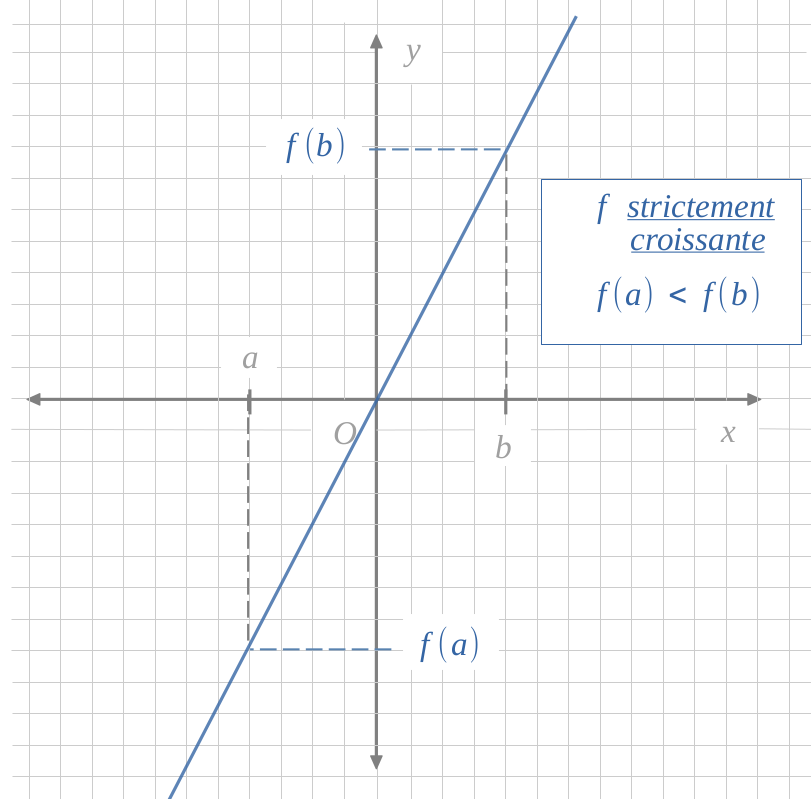
Dans ce cas, on a bien :
et aussi :
Fonctions décroissantes
À l'inverse, on dit qu'une fonction est decroissante si les images sont rangées dans l'ordre inverse des antécédents.
Tableau de variations
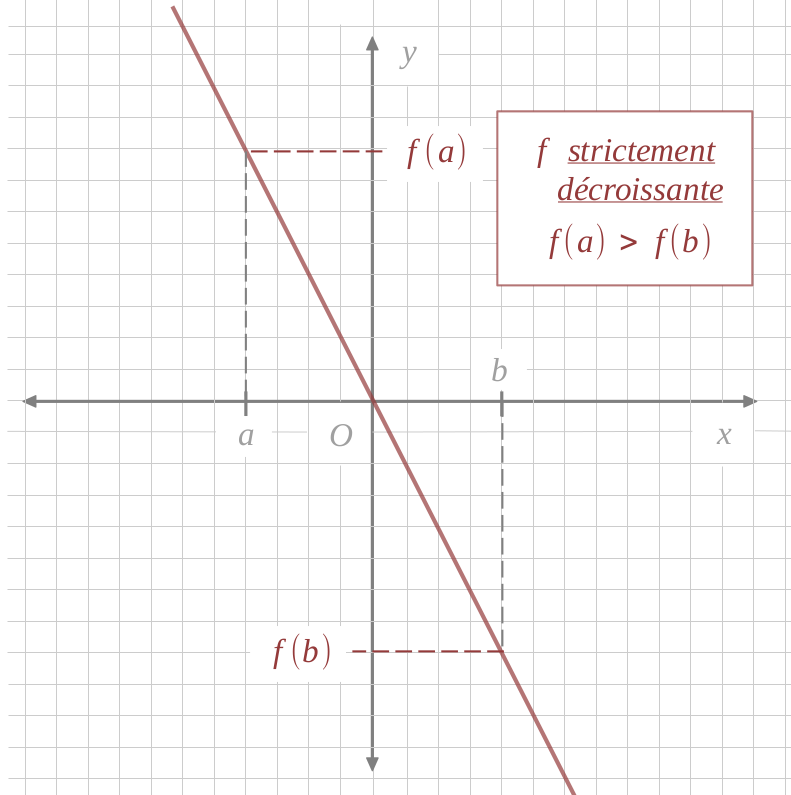
Pour représenter les variations d'une fonction, on pourra utiliser un tableau comme celui-ci :
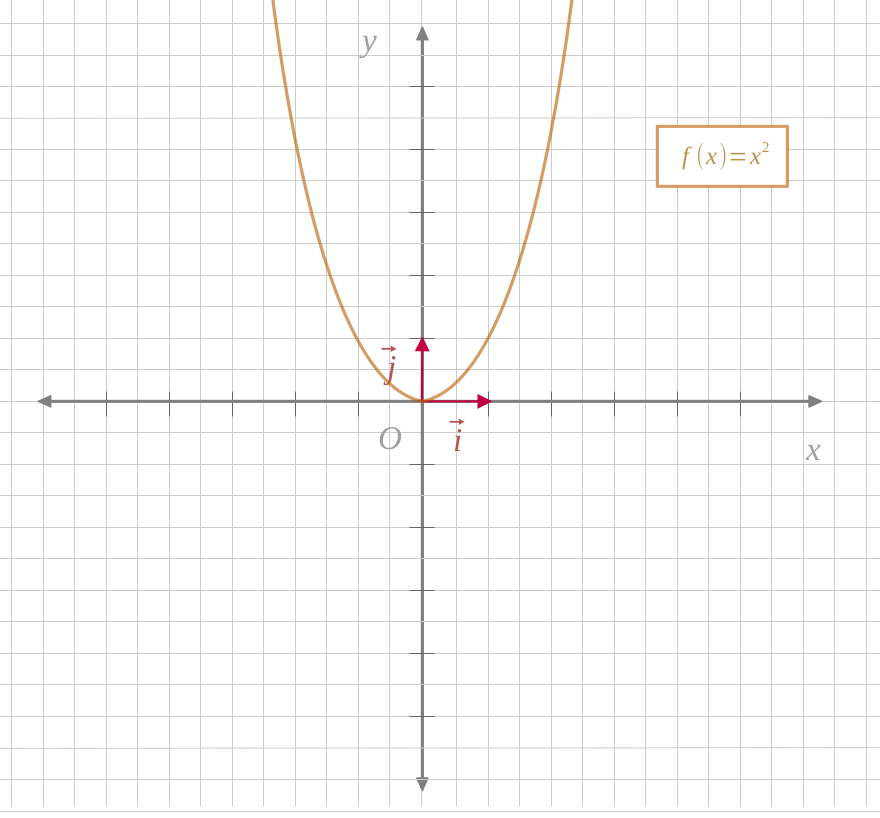
Exemple : la fonction carrée
|
$$ x $$
|
$$ -\infty $$
|
|
$$ 0 $$
|
|
$$ +\infty $$
|
|||
|---|---|---|---|---|---|---|---|---|
|
$$ f(x) = x^2 $$
|
 |
$$ 0 $$
|
|
|||||
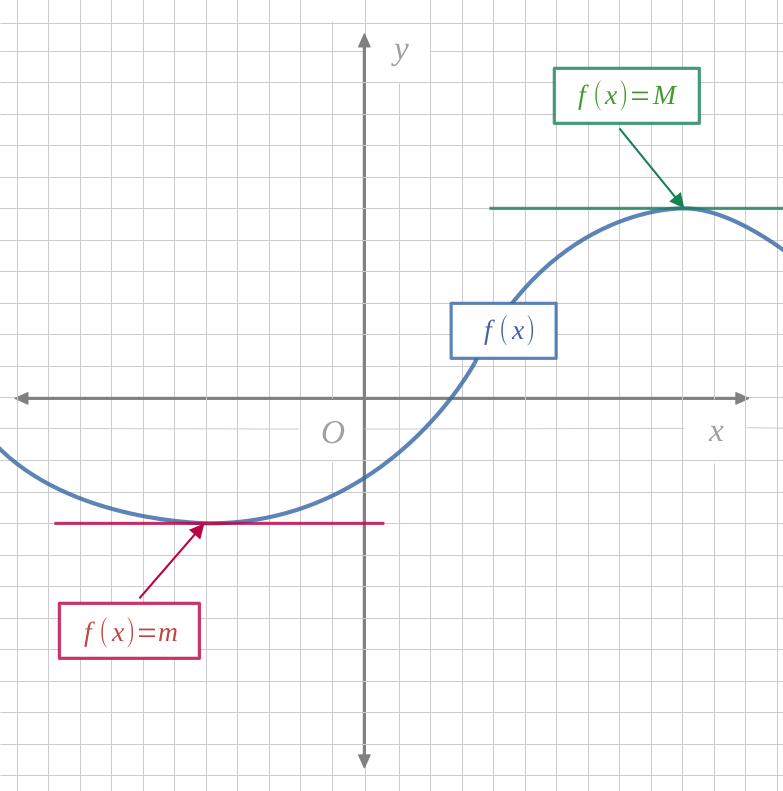
On appelle minimum et maximum d'une fonction \(f\), les points \(m\) et \(M\) tels que :
Index