Représentations géométriques

Lois géométriques du triangle

La somme des angles d'un triangle fait toujours $180°$ $(\pi \ \text{radians}) $.

$$ \alpha + \beta + \gamma = 180 \qquad \bigl[deg \bigr] $$

$$ \alpha + \beta + \gamma = \pi \qquad \bigl[rad \bigr] $$

Dans deux triangles semblables imbriqués $ ABC $ et $ ADE $, où $ADE$ est le plus grand triangle.

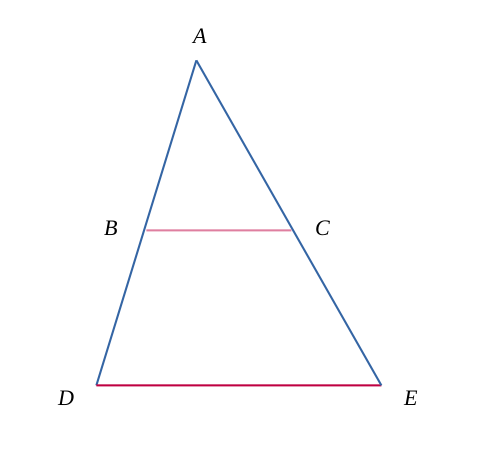
Ou encore dans le cas où les deux triangles sont semblables par l'extérieur (en conservant l'alignement des points précédents).

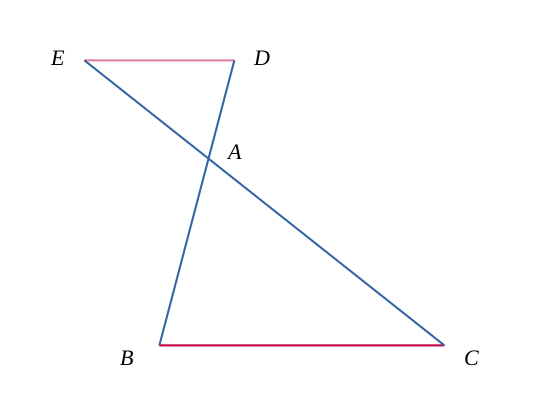
$$ (BC) \parallel (DE) \Longleftrightarrow \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \qquad \bigl(\text{Thalès} \bigr) $$

(deux égalités sur trois sont suffisantes)

Ce théorème permet de :

Dans un triangle rectangle $\bigl \{ a, b, c\bigr\}$ tel que la figure suivante :

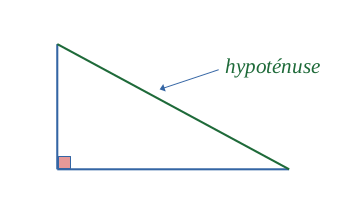
Ce théorème permet de :

$$ (a \perp b) \Longleftrightarrow a^2 + b^2 = c^2 \qquad \bigl(Pythagore \bigr) $$

La formule de Héron est utile pour le calcul d'une aire dans un triangle ordinaire.

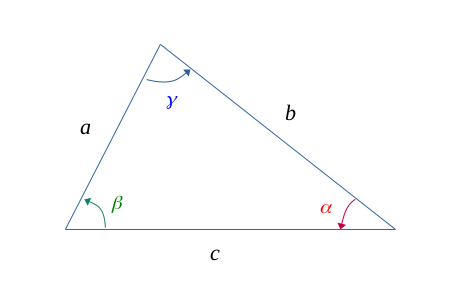
$$ S_{\Delta} = \sqrt{p(p-a)(p-b)(p-c)} \qquad \bigl(\text{Formule de Héron}\bigr) $$

$$ avec \enspace \Biggl \{ \begin{gather*} p : \text{demi-périmètre du triangle} \\ p = \frac{a+b+c}{2} \end{gather*} $$

Cube	Parallélépipède rectangle
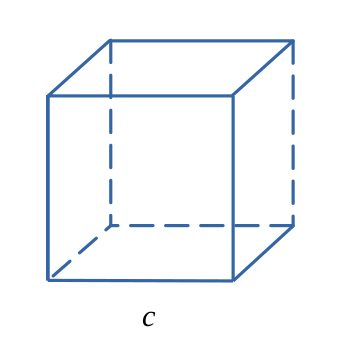
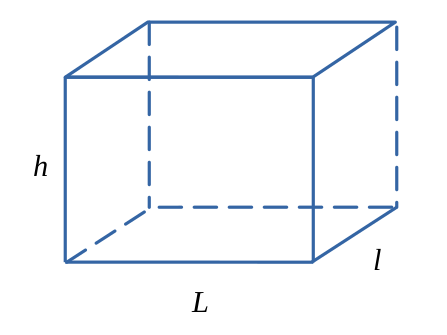
$$ \mathcal{V}= c^3 $$	$$ \mathcal{V} = L \times l \times h $$
Pyramide à base carrée	Cône de révolution
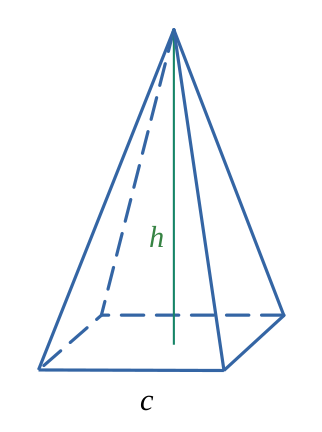
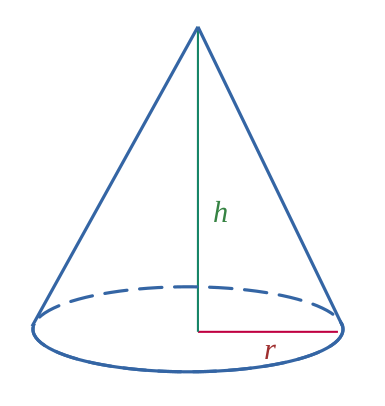
$$ \mathcal{V}= \frac{c^2 \times h}{3} $$	$$ \mathcal{V}= \frac{\pi r^2 \times h}{3} $$
Pyramide (de manière générale)	Cylindre de révolution
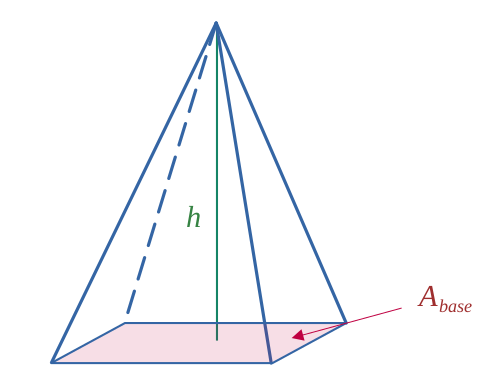
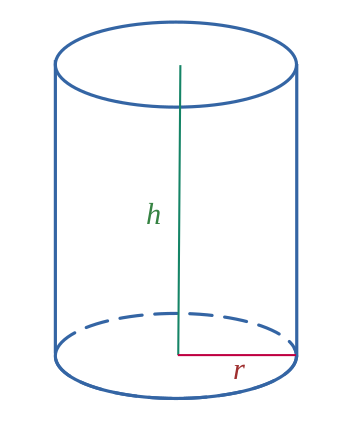
$$ \mathcal{V} = \frac{A_{base} \times h}{3} $$	$$ \mathcal{V}= \pi r^2 \times h $$
Sphère	Calotte sphérique
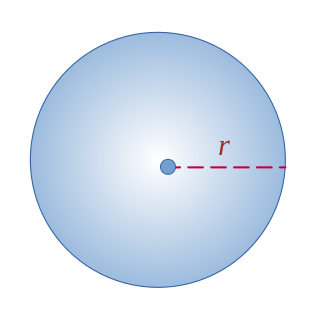
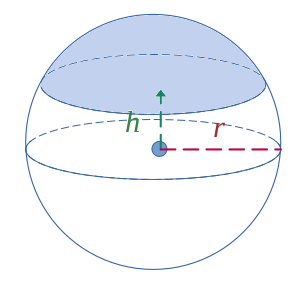
$$ \mathcal{V}=\frac{4}{3} \pi r^3 $$	$$ \mathcal{V} =\pi \left[ r^2 h - \frac{h^3}{3} \right] $$
Demi-sphère tronquée
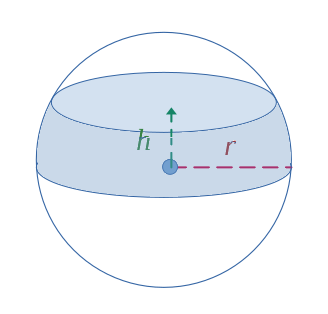
$$ \mathcal{V} =\pi \left[\frac{2r^3}{3} - r^2h + \frac{h^3}{3} \right] $$