Calcul intégral
Intégrale comme aire sous la courbe d'une fonction
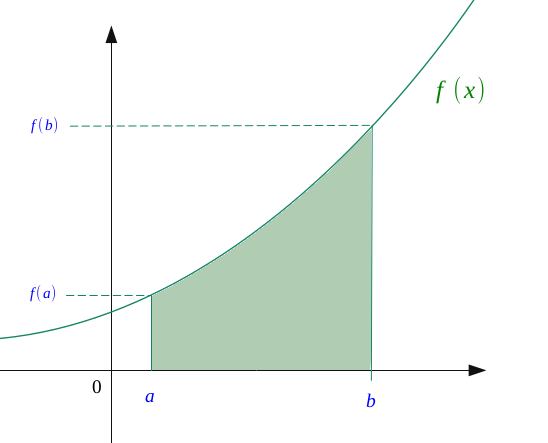
Soit une fonction \(f\) dérivable sur un intervalle \(I = ]a,b[\), et une fonction \(F\) primitive de \(f\).
Alors, l'aire située entre la courbe de \(f\) et l'axe des abscisses vaut :
$$ S_{a,b}= \int_a^b \ f(t) \ dt = F(b) - f(a) $$
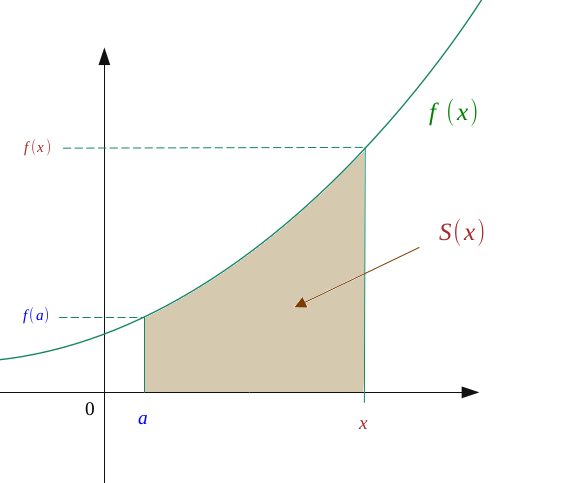
Si la borne supérieure est variable, alors cette intégrale est la primitive de \(f\) qui s'annule en \(a\) :
$$ S(x)= \int_a^x \ f(t) dt $$
Propriétés de l'intégrale
Soit deux fonctions \(f, g\) dérivable sur un intervalle \(I = ]a,b[\), et une fonction \(F\) primitive de \(f\).
Fonction définie par une intégrale
$$ \forall (a, x) \in D_f^2, $$
$$ F(x) = \int_{a}^x f(t) \hspace{0.2em}dt \Longrightarrow F(a) = 0$$
Intégrale de a vers a
$$ \forall a \in D_f, $$
$$ \int_{a}^a f(t) \hspace{0.2em}dt =0 $$
Intégrale de b vers a
$$ \forall (a,b) \in D_f^2, $$
$$ \int_{b}^a f(t) \hspace{0.2em}dt = -\int_{a}^b f(t) \hspace{0.2em}dt $$
Relation de Chasles
$$ \forall (a, \lambda ,b) \in D_f^3, \enspace a \leqslant \lambda \leqslant b, $$
$$ \int_{a}^{\lambda} f(t) \hspace{0.2em}dt + \int_{\lambda}^b f(t) \hspace{0.2em}dt = \int_{a}^b f(t) \hspace{0.2em}dt $$
Linéarité de l'intégrale
$$ \forall (a,b) \in D_f^2, \enspace \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \lambda \int_{a}^b f(t) \hspace{0.2em}dt + \mu \int_{a}^b g(t) \hspace{0.2em}dt $$
L'intégrale d'une combinaison linéaire de fonctions est la combinaison linéaire de l'intégrale de chaque fonction.
Positivité de l'intégrale
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ \enspace f(x) \geqslant 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \geqslant 0 $$
De la même manière, si \( f(x) \leqslant 0 \) sur \( [a, b] \),
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \textcolor{#AF5F5F}{\leqslant} 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \textcolor{#AF5F5F}{\leqslant} 0 $$
Croissance de l'intégrale
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \leqslant g(x) \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \leqslant \int_{a}^b g(t) \hspace{0.2em}dt $$
Valeur moyenne
$$ \forall (a,b) \in D_f^2, $$
$$ \mu = \frac{1}{(b-a)} \int_{a}^b f(t) $$
Théorème de la moyenne
$$ \forall (a,b) \in D_f^2, $$
$$ \exists c \in \hspace{0.05em} ]a,b[, \enspace f(c) = \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt$$
Inégalité de la moyenne
$$ \forall (a,b) \in D_f^2, \ \Bigl[ \forall x \in [a, b], \ m = min\{f\}, \ M = max\{f\} \Bigr], $$
$$ m \hspace{0.2em} \leqslant \hspace{0.2em} \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt \hspace{0.2em} \leqslant \hspace{0.2em} M $$
Méthodes d'intégration
Intégration par parties (IPP)
$$ \forall (a,b) \in D_f^2,$$
$$ \int_{a}^b (f'g) \hspace{0.2em}dt = \Bigl[fg\Bigr]_{a}^b - \int_{a}^b (fg') \hspace{0.2em}dt $$
Avec la dérivée d'un produit, on a :
$$ \left ( f g\right)' = f'g + g'f $$
$$ f'g = ( f g)' - g'f $$
Par suite, grâce à la propriété de linéarité de l'intégrale,
$$ \int_{a}^b (f'g) \hspace{0.2em}dt = \int_{a}^b (fg) -\int_{a}^b (fg') \hspace{0.2em}dt $$
Et,
$$ \int_{a}^b (f'g) \hspace{0.2em}dt = \Bigl[fg\Bigr]_{a}^b -\int_{a}^b (fg') \hspace{0.2em}dt $$
Soit finalement,
$$ \forall (a,b) \in I^2, \enspace a < b, $$
$$ \int_{a}^b (f'g) \hspace{0.2em}dt = \Bigl[fg\Bigr]_{a}^b - \int_{a}^b (fg') \hspace{0.2em}dt $$