


Actuelle

Autre




|
Polygone droit à \(n\) côtés égaux
|
Triangle
|
|---|---|
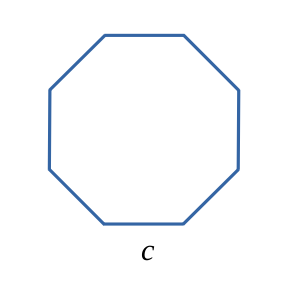
$$ \mathcal{P}= n \times c $$
|
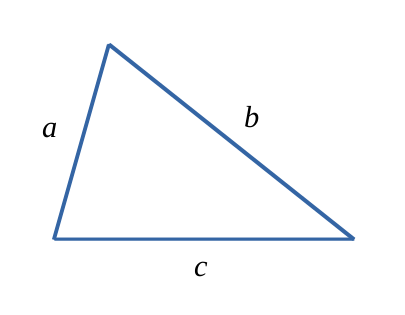
$$ \mathcal{P} = a + b +c $$
|
|
Cercle
|
|
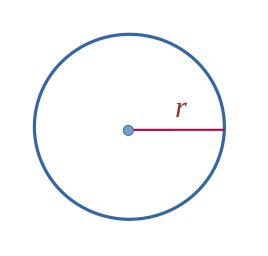
$$ \mathcal{P} =2 \pi r $$
|
|
Carré
|
Rectangle
|
|---|---|
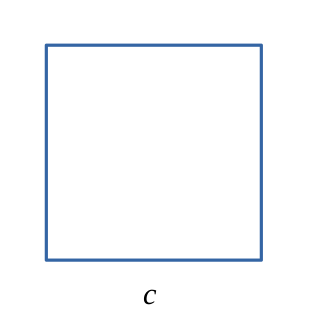
$$ \mathcal{A}= c^2 $$
|
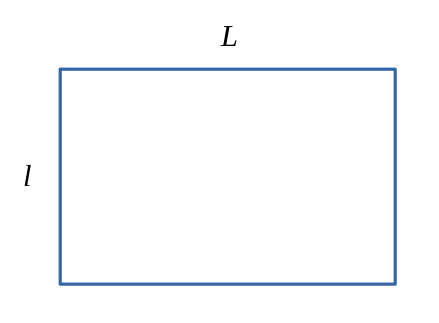
$$ \mathcal{A} = L \times l $$
|
|
Parallélogramme
|
Losange
|
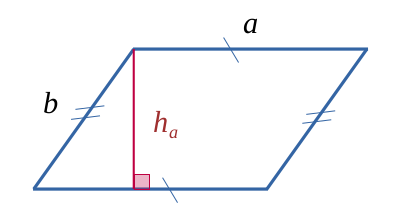
$$ \mathcal{A}= a \times h_a $$
|
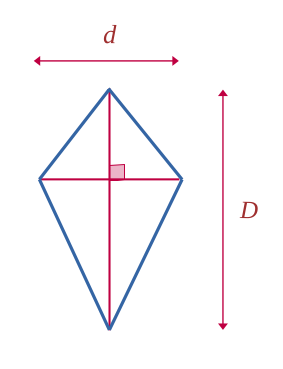
$$ \mathcal{A} = \frac{ D \times d }{2} $$
|
|
Triangle (avec une hauteur)
|
Triangle (avec Héron)
|
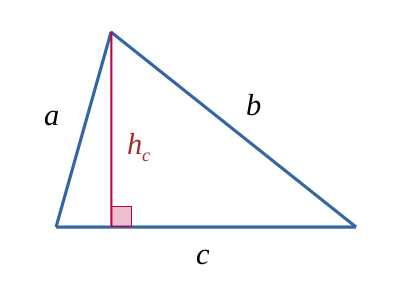
$$ \mathcal{A} = \frac{b\times h_c}{2} $$
|

$$ \mathcal{A} = \sqrt{p(p-a)(p-b)(p-c)} $$
$$\Biggl \{ \begin{gather*} p: \text{demi-périmètre du triangle} \\ \Longrightarrow p = \frac{a+b+c}{2} \end{gather*} $$ |
|
Triangle (avec un angle)
|
Trapèze
|
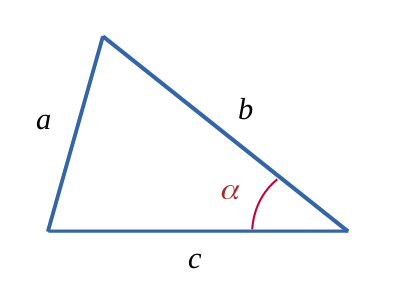
$$ \mathcal{A} = \frac{ sin(\alpha) \times b \times c}{2} $$
|
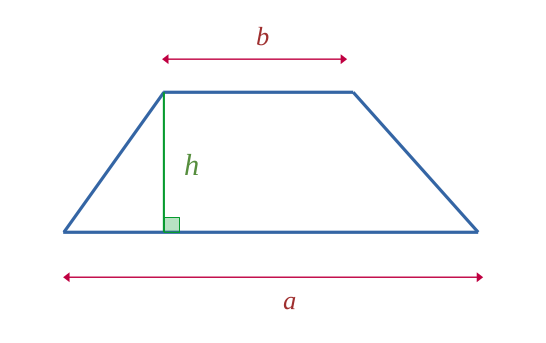
$$ \mathcal{A} = \frac{(a+b) \times h}{2} $$
|
|
Polygone droit à \(n\) côtés égaux
|
|

$$ \mathcal{A} = \frac{n \times c^2}{4 \ tan\left( \frac{\pi}{n} \right) } $$
|
|
|
Cercle
|
Sphère
|

$$ \mathcal{A} = \pi r^2 $$
|
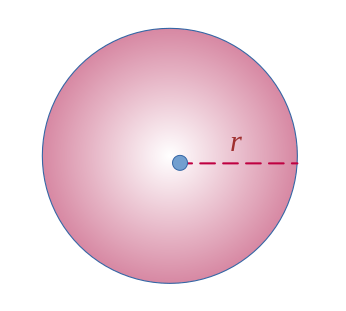
$$ \mathcal{A} = 4\pi r^2 $$
|
|
Demi-sphère tronquée
|
Calotte sphérique
|
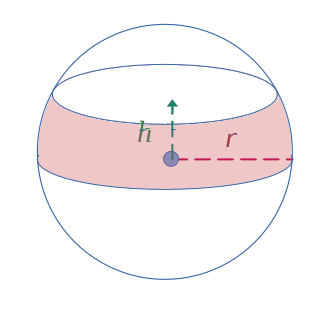
$$ \mathcal{A} = 2\pi r h $$
|
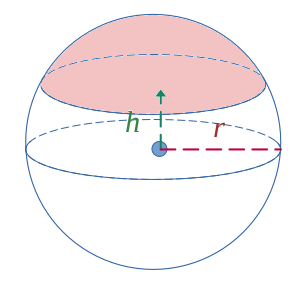
$$ \mathcal{A} = 2\pi r (r-h) $$
|
|
Cube
|
Parallélépipède rectangle
|
|---|---|
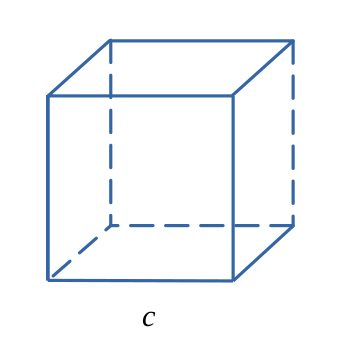
$$ \mathcal{V}= c^3 $$
|
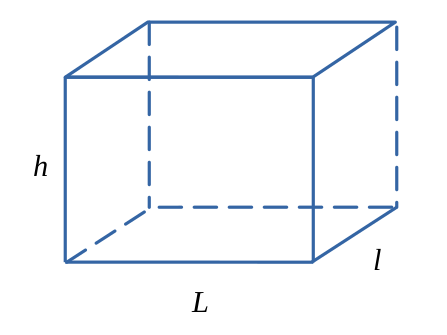
$$ \mathcal{V} = L \times l \times h $$
|
|
Pyramide à base carrée
|
Cône de révolution
|
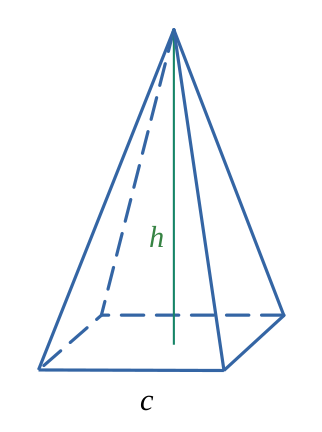
$$ \mathcal{V}= \frac{c^2 \times h}{3} $$
|
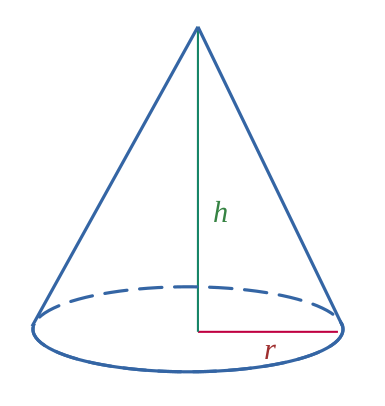
$$ \mathcal{V}= \frac{\pi r^2 \times h}{3} $$
|
|
Pyramide (de manière générale)
|
Cylindre de révolution
|
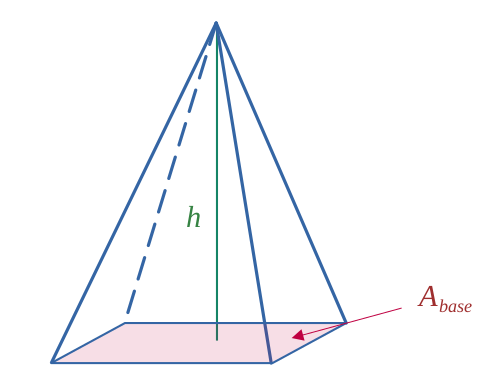
$$ \mathcal{V} = \frac{A_{base} \times h}{3} $$
|
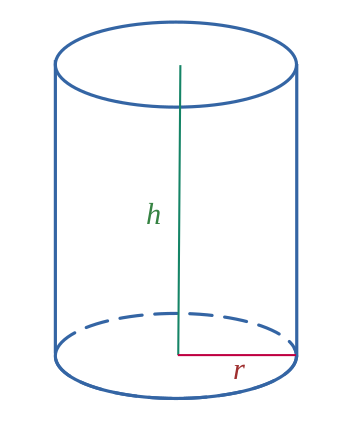
$$ \mathcal{V}= \pi r^2 \times h $$
|
|
Sphère
|
Calotte sphérique
|
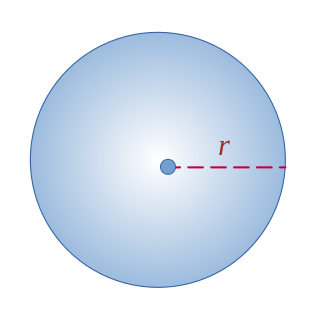
$$ \mathcal{V}=\frac{4}{3} \pi r^3 $$
|
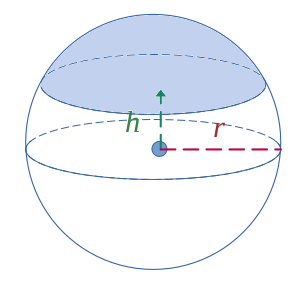
$$ \mathcal{V} =\pi \left[ r^2 h - \frac{h^3}{3} \right] $$
|
|
Demi-sphère tronquée
|
|
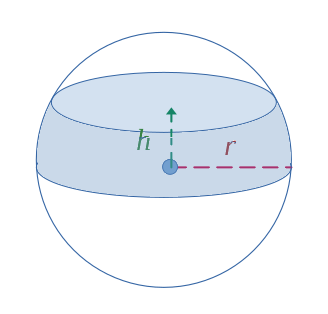
$$ \mathcal{V} =\pi \left[\frac{2r^3}{3} - r^2h + \frac{h^3}{3} \right] $$
|