Vider les textes à trous

Vider les graphiques

Actuelle

Autre

Retour

Imprimer

Théorème de thalès

Connecteurs logiques

Soient $(A, B)$ deux propositions logiques (uniquement deux états : vrai ou faux).

Implication logique

Une implication part d'une cause $(A)$, et engendre une conséquence $(B)$.

$$ A \Longrightarrow B \qquad (\text{Implication}) $$

Contraposée

La contraposée (d'une implication) est la même chose, mais présentée autrement.

$$ non(B) \Longrightarrow non(A) \qquad (\text{Contraposée}) $$

Réciproque

La réciproque (d'une implication) est l'implication inverse. La cause et la conséquence ont été intervertis.

$$ B \Longrightarrow A \qquad (\text{Réciproque}) $$

Exemple :

Prenons les deux propositions suivantes :

$A$ : "il pleut"
$B$ : "je prends mon parapluie en sortant"

Énoncez les implication, contraposée et réciproque à partir de $A$ et $B$ :

Implication :

Contraposée :

Réciproque :

Similarité de deux triangles

Deux triangles semblables

Deux triangles sont dit semblables lorsqu'ils ont :

leurs longueurs respectives proportionnelles;
leurs angles respectivement égaux.

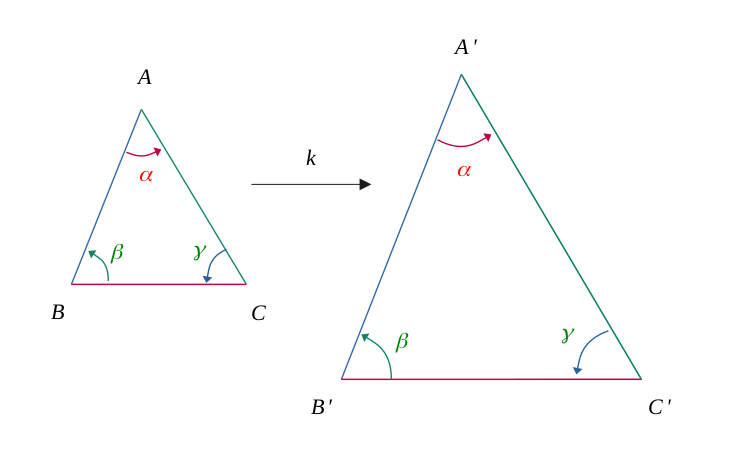
Cela implique alors qu'il existe un rapport $\textcolor{#8A6897}{k}$ entre les longueurs respectives

$$ \begin{Bmatrix} \overline{A'B'} = \textcolor{#8A6897}{k} \times \overline{AB} \\ \overline{B'C'} = \textcolor{#8A6897}{k} \times \overline{BC} \\ \overline{A'C'} = \textcolor{#8A6897}{k} \times \overline{AC} \end{Bmatrix} $$

$$ \Longleftrightarrow $$

$$ \frac{\overline{A'B'}}{\overline{AB}} = \textcolor{#8A6897}{k}, \ \frac{\overline{B'C'}}{\overline{BC}} = \textcolor{#8A6897}{k}, \ \frac{\overline{A'C'}}{\overline{AC}} = \textcolor{#8A6897}{k} $$

Où ce rapport $\textcolor{#8A6897}{k}$ correspondant à :

un agrandissement (si $\textcolor{#8A6897}{k} > 1$);
une réduction (si $\textcolor{#8A6897}{k} < 1$);
une conservation (si $\textcolor{#8A6897}{k} = 1$).

En revanche, les angles eux sont bien conservés ;:

$$ \begin{Bmatrix} \widehat{BAC} = \widehat{B'A'C'} = \textcolor{#8A5757}{\alpha} \\ \widehat{ABC} = \widehat{A'B'C'} = \textcolor{#58814B}{\beta} \\ \widehat{BCA}= \widehat{B'C'A'} = \textcolor{#6F79AB}{\gamma} \end{Bmatrix} $$

Théorème de Thalès et réciproque

Théorème de Thalès

Le théorème de Thalès part de l'hypothèse d'un parallélisme entre deux droites, pour en déduire une égalité entre rapports de longueur.

$$ \bigl( \text{parallélisme} \Longrightarrow \text{égalité} \bigr) $$

Triangles imbriqués par l'intérieur

Dans deux triangles semblables imbriqués $ ABC $ et $ ADE $ tels que la figure suivante :

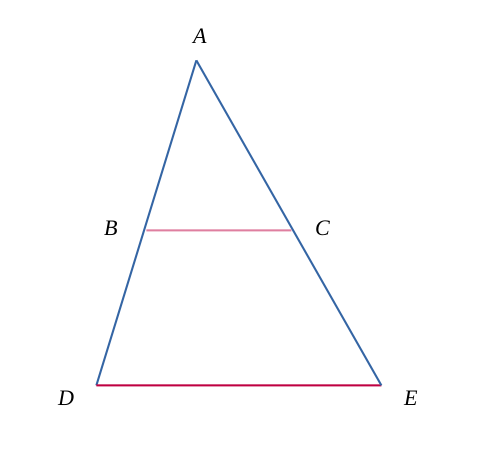
On aura toujours la relation suivante :

$$ (BC) \parallel (DE) \Longrightarrow \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \qquad \bigl(\text{Théorème de Thalès} \bigr) $$

Triangles imbriqués par l'extérieur

Si les triangles sont tels que la figure suivante, imbriqués par l'extérieur :

Deux triangles semblables (imbriqués par l'extérieur)

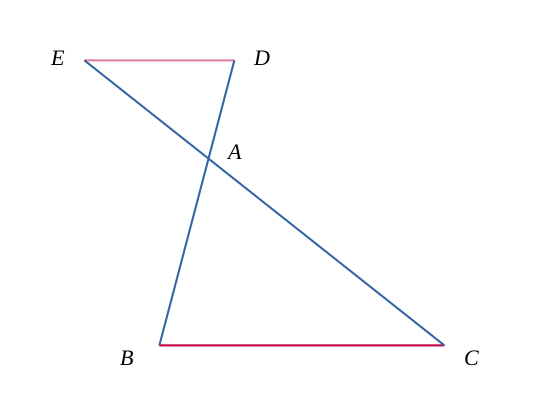
La relation précédente vaut toujours, mais il faut faire attention à bien prendre en compte le changement de côté après dépliage.

Réciproque du théorème de Thalès

La réciproque du théorème de Thalès fait le chemin inverse ; elle part de l'hypothèse d'une égalité entre rapports de longueur, pour en déduire un éventuel parallélisme entre deux droites.

$$ \bigl( \text{égalité} \Longrightarrow \text{parallélisme} \bigr) $$

Dans ce cas, on aura :

$$ \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \Longrightarrow (BC) \parallel (DE) \qquad \bigl(\text{Réciproque du théorème de Thalès} \bigr) $$

Même si en réalité, deux égalités sur trois seulement sont suffisantes (jamais deux sans trois).

$$ \Biggl( \frac{AB}{AD} = \frac{AC}{AE} \Biggr) \text{ ou } \Biggl( \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \text{ ou } \Biggl( \frac{AB}{AD} = \frac{BC}{DE} \Biggr) $$