Afficher en version réduite
Actuelle

Autre
Orthogonalité et produit scalaire
Définitions
Le produit scalaire
Soient \( \vec{u}\) et \( \vec{v}\) deux vecteurs.
On note \(||\vec{u}|| \) et \(||\vec{v}|| \) les normes respectives des vecteurs \( \vec{u}\) et \( \vec{v}\), et \( (\vec{u} , \vec{v})\) l'angle formé par les deux vecteurs.
On appelle le produit scalaire \( \vec{u}.\vec{v} \), le nombre réel résultant de :
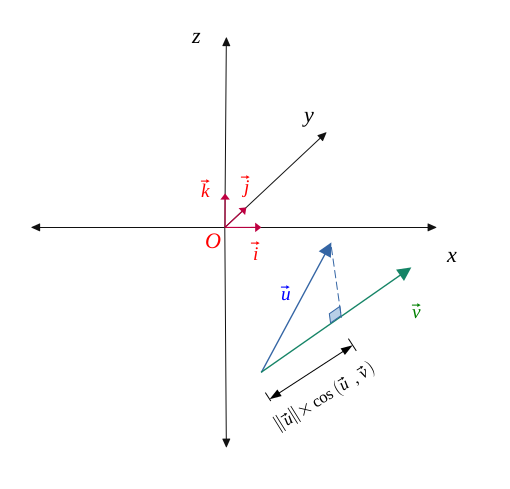
$$ \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) $$
C'est la norme du projeté orthogonal du vecteur \( \vec{u}\) sur le vecteur \( \vec{v}\), multiplié par la norme du vecteur \( \vec{v}\).
Expression analytique du produit scalaire
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
Expression analytique du produit scalaire
Soient \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}\) et \(\vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) deux vecteurs dans un repère orthonormé \( (O, \vec{i}, \vec{j}, \vec{k})\) et telle que la figure suivante :
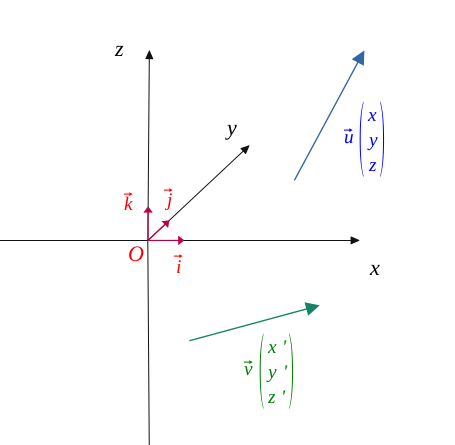
Alors on peut exprimer \(\vec{u} \) et \(\vec{v} \) sous la forme suivante :
$$ \Biggl \{ \begin{gather*}
\vec{u} = x \vec{i} + y \vec{j} +z \vec{k} \\
\vec{v} = x' \vec{i} + y' \vec{j} +z' \vec{k} \end{gather*} $$
Alors le produit scalaire \(\vec{u}.\vec{v} \) vaut :
$$ \vec{u}.\vec{v} = (x \vec{i} + y \vec{j} +z \vec{k}) . ( x' \vec{i} + y' \vec{j} +z' \vec{k}) $$
$$ \vec{u}.\vec{v} = xx'\vec{i}.\vec{i} + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yy''\vec{j}.\vec{j} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} + zz'\vec{k}.\vec{k} $$
$$ \vec{u}.\vec{v} = xx' {|| \vec{i} ||}^2 + yy''{|| \vec{j} ||}^2 + zz'{|| \vec{k} ||}^2 + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} \qquad (1) $$
Les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont par hypothèse nos vecteurs unitaires, alors :
$$ {|| \vec{i} ||}^2 = {|| \vec{j} ||}^2 = {|| \vec{k} ||}^2 = 1 $$
Par ailleurs, étant dans un repère orthonormaux, les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont orthogonaux, alors leur produit scalaire est nul :
$$ \vec{i}.\vec{j} = \vec{i}.\vec{k}= \vec{j}.\vec{k} = 0 $$
Et par commutativité du produit scalaire, on a aussi :
$$ \vec{j}.\vec{i} = \vec{k}.\vec{i}= \vec{k}.\vec{j} = 0 $$
Soit en réécrivant \((1) \),
$$ \vec{u}.\vec{v} = xx' + yy'' + zz' + \hspace{0.1em} \underbrace { xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} } _\text{ \(= \hspace{0.1em} 0\)} $$
Et finalement,
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
Propriétés du produit scalaire
Soit deux fonctions \(f, g\) dérivable sur un intervalle \(I = ]a,b[\), et une fonction \(F\) primitive de \(f\).
Commutativité
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u} . \vec{v} = \vec{v}. \vec{u} $$
Vecteurs orthogonaux
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \text{ et } \vec{v} \ orthogonaux \Longleftrightarrow \vec{u}. \vec{v} = 0 $$
Carré scalaire
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = {|| \vec{u} ||}^2 $$
Bilinéarité
$$ \forall \lambda \in \hspace{0.05em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
Par ailleurs, en effectuant le produit scalaire \( (\lambda\vec{u}).(\mu\vec{v})\), on obtient :
$$ \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).(\mu\vec{v}) = |\lambda| \times |\mu| \times \vec{u}. \vec{v} $$
Distributivité par rapport à l'addition
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ \vec{u}.( \vec{v} + \vec{w}) = \vec{u}.\vec{v} + \vec{u}.\vec{w} $$
Et aussi la distributivé à gauche :
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
Identités remarquables
On a les mêmes formules que les identités remarquables.
$$ \forall (\vec{u}, \vec{v}), $$
$$ (\vec{u} + \vec{v})^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ (\vec{u} - \vec{v})^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2= (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) $$
Expression en fonction des normes
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} + \vec{v} ||}^2 - {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2 \right ) $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} ||}^2 + {|| \vec{v} ||}^2 - {|| \vec{u} -\vec{v} ||}^2 \right ) $$









